문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
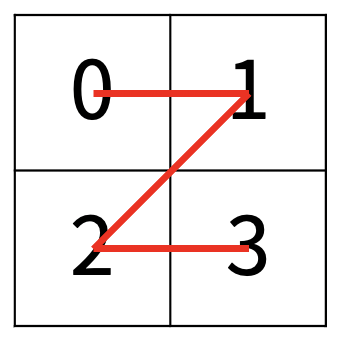
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
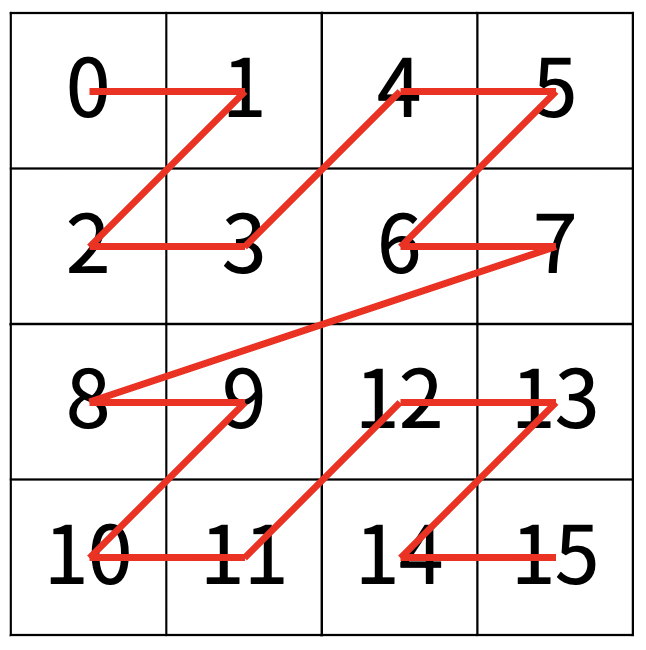
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.
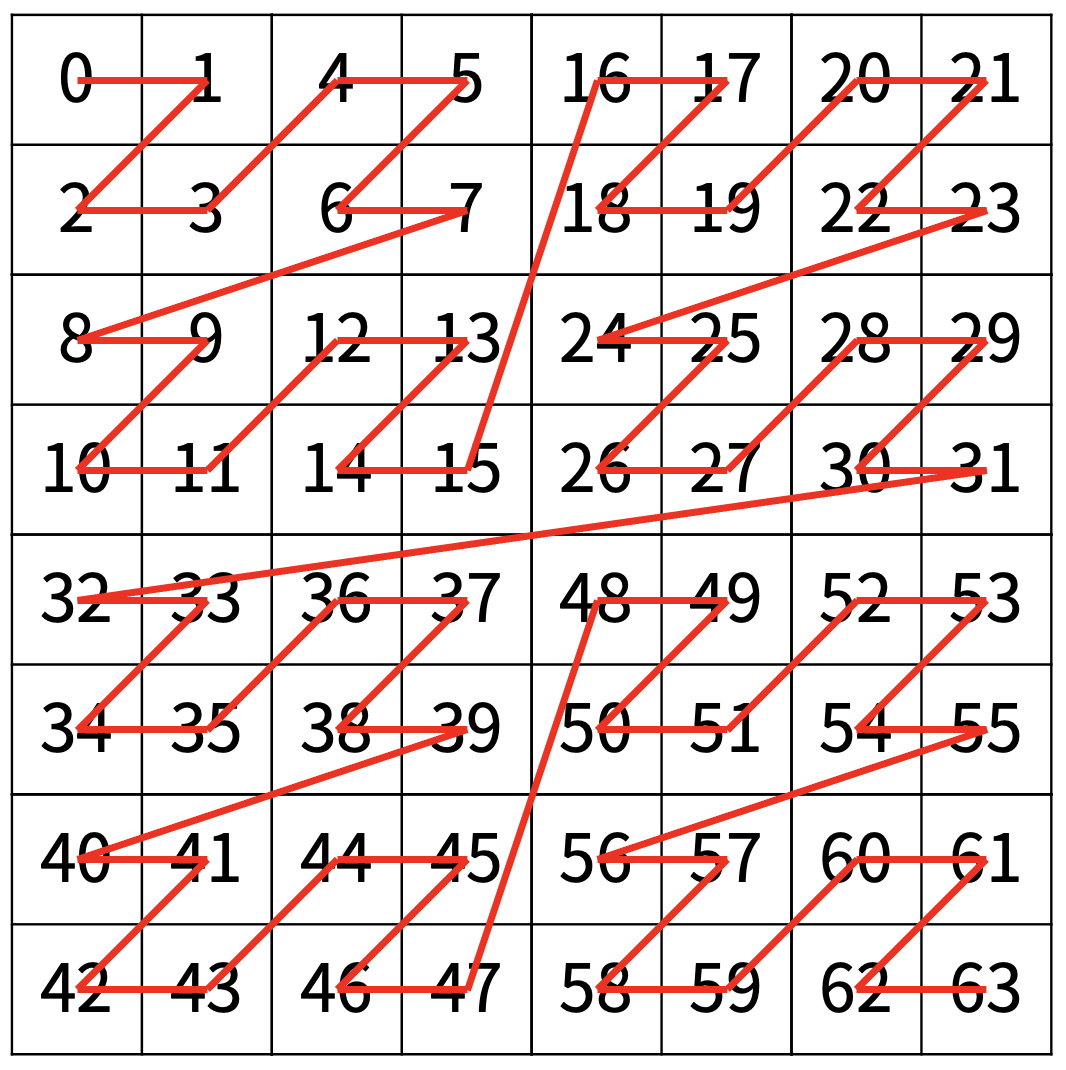
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
접근방법 1
처음에는 count 변수를 두어서 첫 0번째 부터 방문하여서 (r,c)에 해당하는 인덱스를 찾을때 까지 반복했다.
n이 최대 2의 15승인지라 0부터 찾아가기에는 당연히 시간초과가 걸렸다.
#include <iostream>
#include <cmath>
using namespace std;
int n,r,c,count=0;
int result;
void solve(int px, int py, int length){
if(length==2){
if(px==r && py==c){
result = count;
return ;
}
count++;
if(px==r && py+1==c){
result = count;
return ;
}
count++;
if(px+1==r && py==c){
result = count;
return ;
}
count++;
if(px+1==r && py+1==c){
result = count;
return ;
}
count++;
return ;
}
solve(px,py, length/2);
solve(px,py+length/2, length/2);
solve(px+length/2,py, length/2);
solve(px+length/2,py+length/2, length/2);
return ;
}
int main(){
scanf("%d %d %d", &n, &r, &c);
solve(0,0,pow(2,n));
printf("%d\n", result);
}접근방법2
- 0부터 순차적으로 찾기보다는 재귀가 뻗어가는 4부분중에 어느부분에 r,c가 위치하는 지를 판단하여 적극적으로 찾는 방법을 채택했다.
- 각 탐색 색션에 따라 4분면의 인덱스 개수는 (len/2)^2으로 고정되어 있으므로 이를 계산해주면서 재귀를 진행한다.
- ex. n=3인 경우 첫 len은 8이 된다. 이때 각 사분면에 들어갈 수 있는 인덱스 개수는 (8/2)^2 = 16이다.
#include <iostream>
#include <cmath>
using namespace std;
int n,r,c,count=0;
int solve(int x, int y, int len){
if(x==r && y==c) return 0;
if(x<=r && r<x+len/2 && y<=c && c<y+len/2) return 0+solve(x,y,len/2);
if(x<=r && r<x+len/2 && y+len/2<=c && c<y+len) return pow((len/2),2)*1+solve(x,y+len/2,len/2);
if(x+len/2<=r && r<x+len && y<=c && c<y+len/2) return pow((len/2),2)*2+solve(x+len/2,y,len/2);
if(x+len/2<=r && r<x+len && y+len/2<=c && c<y+len) return pow((len/2),2)*3+solve(x+len/2,y+len/2,len/2);
return 0;
}
int main(){
scanf("%d %d %d", &n, &r, &c);
int result = solve(0,0,pow(2,n));
printf("%d\n", result);
}
생각을 더 깊이하여 새로운 방법을 찾아내는 경험은 항상 뿌듯하다.
'알고리즘 문제풀이' 카테고리의 다른 글
| [백준] 1259번 팰린드롬수 c++ (0) | 2022.02.04 |
|---|---|
| [백준] 2475번 검증수 c++ (0) | 2022.02.04 |
| [백준] 2146번 다리 만들기 c++ (0) | 2021.09.05 |
| [백준] 15663 N과 M (9) c++ (0) | 2021.09.04 |
| [백준] 15665번 N과 M (11) c++ (0) | 2021.09.04 |